高中数学第四章-三角函数

考试内容：角的概念的推广．弧度制．
任意角的三角函数．单位圆中的三角函数线．同角三角函数的基本关系式.正弦、余弦的诱导公式．
两角和与差的正弦、余弦、正切．二倍角的正弦、余弦、正切．
正弦函数、余弦函数的图像和性质．周期函数．函数y=Asin(ωx+φ)的图像．正切函数的图像和性质．已知三角函数值求角．
正弦定理．余弦定理．斜三角形解法．
考试要求：
（1）理解任意角的概念、弧度的意义能正确地进行弧度与角度的换算．
（2）掌握任意角的正弦、余弦、正切的定义；了解余切、正割、余割的定义；掌握同角三角函数的基本关系式；掌握正弦、余弦的诱导公式；了解周期函数与最小正周期的意义．
（3）掌握两角和与两角差的正弦、余弦、正切公式；掌握二倍角的正弦、余弦、正切公式．
（4）能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明．
（5）理解正弦函数、余弦函数、正切函数的图像和性质，会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图，理解A.ω、φ的物理意义．
（6）会由已知三角函数值求角，并会用符号arcsinx\arc-cosx\arctanx表示．
（7）掌握正弦定理、余弦定理，并能初步运用它们解斜三角形．
（8）“同角三角函数基本关系式：sin2α+cos2α=1，sinα/cosα=tanα,tanα "cosα=1”．

§04.三角函数知识要点

1. ①与（0°≤＜360°）终边相同的角的集合（角与角的终边重合）：

②终边在x轴上的角的集合：

③终边在y轴上的角的集合：

④终边在坐标轴上的角的集合：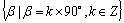

⑤终边在y=x轴上的角的集合：

⑥终边在轴上的角的集合：

⑦若角与角的终边关于x轴对称，则角与角的关系：

⑧若角与角的终边关于y轴对称，则角与角的关系：

⑨若角与角的终边在一条直线上，则角与角的关系：

⑩角与角的终边互相垂直，则角与角的关系：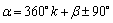

2. 角度与弧度的互换关系：360°=2180°=1°=0.01745 1=57.30°=57°18′

注意：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零.

、弧度与角度互换公式： 1rad＝°≈57.30°=57°18?． 1°＝≈0.01745（rad）

3、弧长公式：. 扇形面积公式：

4、三角函数：设是一个任意角，在的终边上任取（异于原点的）一点P（x,y）P与原点的距离为r，则；；；；；..

5、三角函数在各象限的符号：（一全二正弦，三切四余弦）

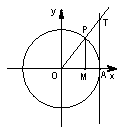
6、三角函数线

正弦线：MP; 余弦线：OM; 正切线： AT.

7. 三角函数的定义域：

8、同角三角函数的基本关系式：

9、诱导公式：

“奇变偶不变，符号看象限”

三角函数的公式：（一）基本关系

公式组二公式组三

公式组四公式组五公式组六

（二）角与角之间的互换

公式组一公式组二

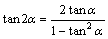
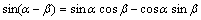
公式组三公式组四公式组五

,,,.

10. 正弦、余弦、正切、余切函数的图象的性质：

注意：①与的单调性正好相反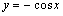；与的单调性也同样相反.一般地，若在上递增（减），则在上递减（增）.

②与的周期是.

③或（）的周期.

的周期为2（，如图，翻折无效）.

④的对称轴方程是（），对称中心（）；的对称轴方程是（），对称中心（）；的对称中心（）.

⑤当·；·.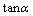

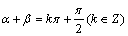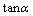⑥与是同一函数,而是偶函数，则

.

⑦函数在上为增函数.（×） [只能在某个单调区间单调递增. 若在整个定义域，为增函数，同样也是错误的].

⑧定义域关于原点对称是具有奇偶性的必要不充分条件.（奇偶性的两个条件：一是定义域关于原点对称（奇偶都要），二是满足奇偶性条件，偶函数：，奇函数：）

奇偶性的单调性：奇同偶反. 例如：是奇函数，是非奇非偶.（定义域不关于原点对称）

奇函数特有性质：若的定义域，则一定有.（的定义域，则无此性质）

⑨不是周期函数；为周期函数（）；

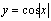是周期函数（如图）；为周期函数（）；

的周期为（如图），并非所有周期函数都有最小正周期，例如：

.

⑩有.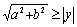

11、三角函数图象的作法：

１）、几何法：

２）、描点法及其特例——五点作图法（正、余弦曲线），三点二线作图法（正、余切曲线）.

３）、利用图象变换作三角函数图象．

三角函数的图象变换有振幅变换、周期变换和相位变换等．

函数y＝Asin（ωx＋φ）的振幅|A|，周期，频率，相位初相（即当x＝0时的相位）．（当A＞0，ω＞0 时以上公式可去绝对值符号），

由y＝sinx的图象上的点的横坐标保持不变，纵坐标伸长（当|A|＞1）或缩短（当0＜|A|＜1）到原来的|A|倍，得到y＝Asinx的图象，叫做振幅变换或叫沿y轴的伸缩变换．（用y/A替换y）

由y＝sinx的图象上的点的纵坐标保持不变，横坐标伸长（0＜|ω|＜1）或缩短（|ω|＞1）到原来的倍，得到y＝sinω x的图象，叫做周期变换或叫做沿x轴的伸缩变换．(用ωx替换x)

由y＝sinx的图象上所有的点向左（当φ＞0）或向右（当φ＜0）平行移动｜φ｜个单位，得到y＝sin（x＋φ）的图象，叫做相位变换或叫做沿x轴方向的平移．(用x＋φ替换x)

由y＝sinx的图象上所有的点向上（当b＞0）或向下（当b＜0）平行移动｜b｜个单位，得到y＝sinx＋b的图象叫做沿y轴方向的平移．（用y+(-b)替换y）

由y＝sinx的图象利用图象变换作函数y＝Asin（ωx＋φ）（A＞0，ω＞0）（x∈R）的图象，要特别注意：当周期变换和相位变换的先后顺序不同时，原图象延x轴量伸缩量的区别。

4、反三角函数：

函数y＝sinx，的反函数叫做反正弦函数，记作y＝arcsinx，它的定义域是［－1，1］，值域是．

函数y＝cosx，（x∈［0，π］）的反应函数叫做反余弦函数，记作y＝arccosx，它的定义域是［－1，1］，值域是［0，π］．

函数y＝tanx，的反函数叫做反正切函数，记作y＝arctanx，它的定义域是（－∞，＋∞），值域是．

函数y＝ctgx，［x∈（0，π）］的反函数叫做反余切函数，记作y＝arcctgx，它的定义域是（－∞，＋∞），值域是（0，π）．

II.竞赛知识要点

一、反三角函数.

1. 反三角函数：⑴反正弦函数是奇函数，故，（一定要注明定义域，若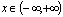，没有与一一对应，故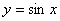无反函数）

注：，，.

⑵反余弦函数非奇非偶，但有，.

注：①，，.

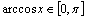②是偶函数，非奇非偶，而和为奇函数.

⑶反正切函数：，定义域，值域（），是奇函数，

，.

注：，.

⑷反余切函数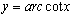：，定义域，值域（），是非奇非偶.

，.

注：①，.

②与互为奇函数，同理为奇而与非奇非偶但满足.

⑵ 正弦、余弦、正切、余切函数的解集：

的取值范围 解集的取值范围 解集

①的解集②的解集

＞1＞1

=1=1

＜1＜1

③的解集：③的解集：

二、三角恒等式.

组一

组二

组三三角函数不等式

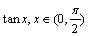
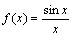＜＜在上是减函数

若，则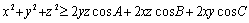

第二篇：三角函数知识点总结

第六章三角函数

一、基础知识

定义1角，一条射线绕着它的端点旋转得到的图形叫做角。若旋转方向为逆时针方向，则角为正角，若旋转方向为顺时针方向，则角为负角，若不旋转则为零角。角的大小是任意的。

定义2角度制，把一周角360等分，每一等价为一度，弧度制：把等于半径长的圆弧所对的圆心角叫做一弧度。360度=2π弧度。若圆心角的弧长为L，则其弧度数的绝对值|α|=,其中r是圆的半径。

定义3三角函数，在直角坐标平面内，把角α的顶点放在原点，始边与x轴的正半轴重合，在角的终边上任意取一个不同于原点的点P，设它的坐标为（x,y），到原点的距离为r,则正弦函数sinα=,余弦函数cosα=,正切函数tanα=，余切函数cotα=，

定理1同角三角函数的基本关系式，

倒数关系：tanα=,商数关系：tanα=；

乘积关系：tanα×cosα=sinα,cotα×sinα=cosα；平方关系：sin2α+cos2α=1,tan2α+1=sec2α,cot2α+1=csc2α.

定理2诱导公式（Ⅰ）sin(α+π)=-sinα,cos(π+α)=-cosα,tan(π+α)=tanα;

（Ⅱ）sin(-α)=-sinα,cos(-α)=cosα,tan(-α)=-tanα;

（Ⅲ）sin(π-α)=sinα,cos(π-α)=-cosα,tan=(π-α)=-tanα; （

Ⅳ）sin=cosα,cos=sinα（奇变偶不变，符号看象限）。

定理3正弦函数的性质，根据图象可得y=sinx（x∈R）的性质如下。单调区间：在区间上为增函数，在区间上为减函数，最小正周期为2. 奇偶数. 有界性：当且仅当x=2kx+时，y取最大值1，当且仅当x=3k-时,y取最小值-1。对称性：直线x=k+均为其对称轴，点（k, 0）均为其对称中心，值域为[-1，1]。这里k∈Z.

定理4 余弦函数的性质，根据图象可得y=cosx(x∈R)的性质。单调区间：在区间[2kπ, 2kπ+π]上单调递减，在区间[2kπ-π, 2kπ]上单调递增。最小正周期为2π。奇偶性：偶函数。对称性：直线x=kπ均为其对称轴，点均为其对称中心。有界性：当且仅当x=2kπ时，y取最大值1；当且仅当x=2kπ-π时，y取最小值-1。值域为[-1，1]。这里k∈Z.

定理5 正切函数的性质：由图象知奇函数y=tanx(xkπ+)在开区间(kπ-,kπ+)上为增函数, 最小正周期为π，值域为（-∞，+∞），点（kπ，0），（kπ+，0）均为其对称中心。

定理6 两角和与差的基本关系式：cos(αβ)=cosαcosβsinαsinβ,sin(αβ)=sinαcosβcosαsinβ;tan(αβ)=

定理7 和差化积与积化和差公式:

sinα+sinβ=2sincos,sinα-sinβ=2sincos,

cosα+cosβ=2coscos,cosα-cosβ=-2sinsin,

sinαcosβ=[sin(α+β)+sin(α-β)],cosαsinβ=[sin(α+β)-sin(α-β)],

cosαcosβ=[cos(α+β)+cos(α-β)],sinαsinβ=-[cos(α+β)-cos(α-β)].

定理8 倍角公式:sin2α=2sinαcosα,cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α,

tan2α=

定理9 半角公式:sin=,cos=,

tan==

定理10 万能公式:,,

定理11 辅助角公式：如果a,b是实数且a2+b20，则取始边在x轴正半轴，终边经过点(a,b)的一个角为β，则sinβ=,cosβ=，对任意的角α.

asinα+bcosα=sin(α+β).

定理12 正弦定理：在任意△ABC中有，其中a,b,c分别是角A，B，C的对边，R为△ABC外接圆半径。

定理13 余弦定理：在任意△ABC中有a2=b2+c2-2bcosA，其中a,b,c分别是角A，B，C的对边。

定理14 图象之间的关系：y=sinx的图象经上下平移得y=sinx+k的图象；经左右平移得y=sin(x+)的图象（相位变换）；纵坐标不变，横坐标变为原来的，得到y=sin()的图象（周期变换）；横坐标不变，纵坐标变为原来的A倍，得到y=Asinx的图象（振幅变换）；y=Asin(x+)(＞0)的图象（周期变换）；横坐标不变，纵坐标变为原来的A倍，得到y=Asinx的图象（振幅变换）；y=Asin(x+)(,＞0)(|A|叫作振幅)的图象向右平移个单位得到y=Asinx的图象。

定义4 函数y=sinx的反函数叫反正弦函数，记作y=arcsinx(x∈[-1, 1])，函数y=cosx(x∈[0, π]) 的反函数叫反余弦函数，记作y=arccosx(x∈[-1, 1]). 函数y=tanx的反函数叫反正切函数。记作y=arctanx(x∈[-∞, +∞]).y=cosx(x∈[0, π])的反函数称为反余切函数，记作y=arccotx(x∈[-∞, +∞]).

定理15 三角方程的解集，如果a∈(-1,1)，方程sinx=a的解集是{x|x=nπ+(-1)narcsina,n∈Z}。方程cosx=a的解集是{x|x=2kxarccosa,k∈Z}. 如果a∈R，方程tanx=a的解集是{x|x=kπ+arctana,k∈Z}。恒等式：arcsina+arccosa=；arctana+arccota=.

定理16 若，则sinx＜x＜tanx.

二、方法与例题

1．结合图象解题。

例1 求方程sinx=lg|x|的解的个数。

【解】在同一坐标系内画出函数y=sinx与y=lg|x|的图象（见图），由图象可知两者有6个交点，故方程有6个解。

2．三角函数性质的应用。

例2 设x∈(0, π), 试比较cos(sinx)与sin(cosx)的大小。

【解】 若，则cosx≤1且cosx＞-1，所以cos，

所以sin(cosx) ≤0,又0inx≤1, 所以cos(sinx)＞0，

所以cos(sinx)＞sin(cosx).

若，则因为sinx+cosx=(sinxcos+sincosx)=sin(x+)≤＜，

所以0inx＜-cosx＜，

所以cos(sinx)＞cos(-cosx)=sin(cosx).

综上，当x∈(0,π)时，总有cos(sinx)in(cosx).

例3 已知α，β为锐角，且x·（α+β-）＞0，求证：

【证明】 若α+β＞，则x＞0，由α＞-β＞0得cosα＜cos(-β)=sinβ,

所以0＜＜1，又sinα＞sin(-β)=cosβ, 所以0＜＜1，

所以

若α+β＜，则x＜0，由0＜α＜-β＜得cosα＞cos(-β)=sinβ＞0,

所以＞1。又0inαin(-β)=cosβ，所以＞1，

所以，得证。

注：以上两例用到了三角函数的单调性和有界性及辅助角公式，值得注意的是角的讨论。

3．最小正周期的确定。

例4 求函数y=sin(2cos|x|)的最小正周期。

【解】 首先，T=2π是函数的周期（事实上，因为cos(-x)=cosx，所以co|x|=cosx）；其次，当且仅当x=kπ+时，y=0（因为|2cosx|≤2＜π）,

所以若最小正周期为T0，则T0=mπ, m∈N+，又sin(2cos0)=sin2sin(2cosπ)，所以T0=2π。

4．三角最值问题。

例5 已知函数y=sinx+，求函数的最大值与最小值。

【解法一】 令sinx=,

则有y=

因为，所以，

所以≤1，

所以当，即x=2kπ-(k∈Z)时，ymin=0，

当，即x=2kπ+(k∈Z)时，ymax=2.

【解法二】 因为y=sinx+,

=2（因为(a+b)2≤2(a2+b2)），

且|sinx|≤1≤，所以0≤sinx+≤2，

所以当=sinx，即x=2kπ+(k∈Z)时,ymax=2，

当=-sinx，即x=2kπ-(k∈Z)时,ymin=0。

例6 设0＜＜π，求sin的最大值。

【解】因为0＜＜π，所以，所以sin＞0,cos＞0.

所以sin（1+cos）=2sin·cos2=≤=

当且仅当2sin2=cos2, 即tan=,=2arctan时，sin(1+cos)取得最大值。

例7 若A，B，C为△ABC三个内角，试求sinA+sinB+sinC的最大值。

【解】 因为sinA+sinB=2sincos, ①

sinC+sin, ②

又因为，③

由①，②，③得sinA+sinB+sinC+sin≤4sin,

所以sinA+sinB+sinC≤3sin=,

当A=B=C=时，（sinA+sinB+sinC）max=.

注：三角函数的有界性、|sinx|≤1、|cosx|≤1、和差化积与积化和差公式、均值不等式、柯西不等式、函数的单调性等是解三角最值的常用手段。

5．换元法的使用。

例8 求的值域。

【解】 设t=sinx+cosx=

因为

所以

又因为t2=1+2sinxcosx,

所以sinxcosx=，所以，

所以

因为t-1，所以，所以y-1.

所以函数值域为

例9 已知a0=1,an=(n∈N+)，求证：an＞.

【证明】 由题设an＞0，令an=tanan,an∈，则

an=

因为，an∈，所以an=，所以an=

又因为a0=tana1=1，所以a0=，所以·。

又因为当0＜x＜时，tanx＞x，所以

注：换元法的关键是保持换元前后变量取值范围的一致性。

另外当x∈时，有tanx＞x＞sinx，这是个熟知的结论，暂时不证明，学完导数后，证明是很容易的。

6．图象变换：y=sinx(x∈R)与y=Asin(x+)(A,,＞0).

由y=sinx的图象向左平移个单位，然后保持横坐标不变，纵坐标变为原来的A倍，然后再保持纵坐标不变，横坐标变为原来的，得到y=Asin(x+)的图象；也可以由y=sinx的图象先保持横坐标不变，纵坐标变为原来的A倍，再保持纵坐标不变，横坐标变为原来的，最后向左平移个单位，得到y=Asin(x+)的图象。

例10 例10 已知f(x)=sin(x+)(＞0, 0≤≤π)是R上的偶函数，其图象关于点对称，且在区间上是单调函数，求和的值。

【解】 由f(x)是偶函数，所以f(-x)=f(x)，所以sin(+)=sin(-x+)，所以cossinx=0，对任意x∈R成立。

又0≤≤π，解得=，

因为f(x)图象关于对称，所以=0。

取x=0，得=0，所以sin

所以(k∈Z)，即=(2k+1) (k∈Z).

又＞0，取k=0时，此时f(x)=sin(2x+)在[0，]上是减函数；

取k=1时，=2，此时f(x)=sin(2x+)在[0，]上是减函数；

取k=2时，≥，此时f(x)=sin(x+)在[0，]上不是单调函数，

综上，=或2。

7．三角公式的应用。

例11 已知sin(α-β)=，sin(α+β)=-，且α-β∈，α+β∈，求sin2α,cos2β的值。

【解】 因为α-β∈，所以cos(α-β)=-

又因为α+β∈，所以cos(α+β)=

所以sin2α=sin[(α+β)+(α-β)]=sin(α+β)cos(α-β)+cos(α+β)sin(α-β)=,

cos2β=cos[(α+β)-(α-β)]=cos(α+β)cos(α-β)+sin(α+β)sin(α-β)=-1.

例12 已知△ABC的三个内角A，B，C成等差数列，且，试求的值。

【解】 因为A=1200-C，所以cos=cos(600-C)，

又由于

=，

所以=0。

解得或。

又＞0，所以。

例13 求证：tan20+4cos70.

【解】tan20+4cos70=+4sin20

三、基础训练题

1．已知锐角x的终边上一点A的坐标为(2sin3, -2cos3)，则x的弧度数为___________。

2．适合-2cscx的角的集合为___________。

3．给出下列命题：（1）若αβ，则sinαsinβ；（2）若sinαsinβ,则αβ；（3）若sinα＞0，则α为第一或第二象限角；（4）若α为第一或第二象限角，则sinα＞0. 上述四个命题中，正确的命题有__________个。

4．已知sinx+cosx=(x∈(0, π))，则cotx=___________。

5．简谐振动x1=Asin和x2=Bsin叠加后得到的合振动是x=___________。

6．已知3sinx-4cosx=5sin(x+1)=5sin(x-2)=5cos(x+3)=5cos(x-4)，则1，2，3，4分别是第________象限角。

7．满足sin(sinx+x)=cos(cosx-x)的锐角x共有________个。

8．已知，则=___________。

9．=___________。

10．cot15cos25cot35cot85=___________。

11．已知α,β∈(0, π),tan,sin(α+β)=，求cosβ的值。

12．已知函数f(x)=在区间上单调递减，试求实数m的取值范围。

四、高考水平训练题

1．已知一扇形中心角是a,所在圆半径为R，若其周长为定值c(c＞0)，当扇形面积最大时，a=__________.

2. 函数f(x)=2sinx(sinx+cosx)的单调递减区间是__________.

3. 函数的值域为__________.

4. 方程=0的实根个数为__________.

5. 若sina+cosa=tana,a，则__________a（填大小关系）.

6. (1+tan1)(1+tan2)…(1+tan44)(1+tan45)=__________.

7. 若0＜y≤x＜且tanx=3tany，则x-y的最大值为__________.

8.=__________.

9.·cos·cos·cos·cos=__________.

10.cos271+cos71cos49+cos249=__________.

11. 解方程：sinx+2sin2x=3+sin3x.

12. 求满足sin(x+sinx)=cos(x-cosx)的所有锐角x.

13. 已知f(x)=(kA0,k∈Z, 且A∈R)，（1）试求f(x)的最大值和最小值；（2）若A＞0,k=-1，求f(x)的单调区间；（3）试求最小正整数k，使得当x在任意两个整数（包括整数本身）间变化时，函数f(x)至少取得一次最大值和一次最小值。

五、联赛一试水平训练题（一）

1．若x,y∈R，则z=cosx2+cosy2-cosxy的取值范围是____________.

2．已知圆x2+y2=k2至少盖住函数f(x)=的一个最大值点与一个最小值点，则实数k的取值范围是____________.

3．f()=5+8cos+4cos2+cos3的最小值为____________.

4．方程sinx+cosx+a=0在（0，2π）内有相异两实根α，β，则α+β=____________.

5．函数f(x)=|tanx|+|cotx|的单调递增区间是____________.

6．设sina＞0＞cosa, 且sin＞cos，则的取值范围是____________.

7．方程tan5x+tan3x=0在[0，π]中有__________个解.

8．若x,y∈R, 则M=cosx+cosy+2cos(x+y)的最小值为____________.

9．若0＜＜,m∈N+, 比较大小：(2m+1)sinm(1-sin)__________1-sin2m+1.

10．cot70+4cos70=____________.

11. 在方程组中消去x,y，求出关于a,b,c的关系式。

12．已知α，β，γ，且cos2α+cos2β+cos2γ=1，求tanαtanβtanγ的最小值。

13．关于x,y的方程组有唯一一组解，且sinα,sinβ,sinγ互不相等，求sinα+sinβ+sinγ的值。

14．求满足等式sinxy=sinx+siny的所有实数对（x,y）,x,y.

联赛一试水平训练题（二）

1．在平面直角坐标系中，函数f(x)=asinax+cosax(a＞0)在一个最小正周期长的区间上的图象与函数g(x)=的图象所围成的封闭图形的面积是__________.

2．若，则y=tan-tan+cos的最大值是__________.

3．在△ABC中，记BC=a,CA=b,AB=c, 若9a2+9b2-19c2=0，则=__________.

4．设f(x)=x2-πx, α=arcsin, β=arctan, γ=arccos, δ=arccot, 将f(α),f(β),f(γ),f(δ)从小到大排列为__________.

5．logsin1cos1=a,logsin1tan1=b,logcos1sin1=c,logcos1tan1=d。将a,b,c, d从小到大排列为__________.

6．在锐角△ABC中，cosA=cosαsinβ,cosB=cosβsinγ,cosC=cosγsinα，则tanα·tanβ·tanγ=__________.

7．已知矩形的两边长分别为tan和1+cos(0＜＜π)，且对任何x∈R,f(x)=sin·x2+·x+cos≥0，则此矩形面积的取值范围是__________.

8．在锐角△ABC中，sinA+sinB+sinC的取值范围是__________.

9．已知当x∈[0, 1]，不等式x2cos-x(1-x)+(1-x)2sin＞0恒成立，则的取值范围是__________.

10．已知sinx+siny+sinz=cosx+cosy+cosz=0，则cos2x+cos2y+cos2z=__________.

11．已知a1,a2, …,an是n个实常数，考虑关于x的函数：f(x)=cos(a1+x)+cos(a2+x) +…+cos(an+x)。求证：若实数x1,x2满足f(x1)=f(x2)=0，则存在整数m，使得x2-x1=mπ.

12．在△ABC中，已知，求证：此三角形中有一个内角为。

13．求证：对任意自然数n, 均有|sin1|+|sin2|+…+|sin(3n-1)|+|sin3n|＞.

六、联赛二试水平训练题

1．已知x＞0,y＞0, 且x+y＜π，求证：w(w-1)sin(x+y)+w(sinx-siny)+siny＞0①（w∈R）.

2. 已知a为锐角，n≥2,n∈N+，求证：≥2n-2+1.

3. 设x1,x2,…,xn,…,y1,y2,…,yn,…满足x1=y1=,xn+1=xn+,yn+1=，求证：2＜xnyn＜3(n≥2).

4．已知α，β，γ为锐角，且cos2α+cos2β+cos2γ=1，求证；π＜α+β+γ＜π.

5．求实数a的取值范围，使得对任意实数x和任意，恒有(x+3+2sincos)2+(x+asin+asin)2≥

6. 设n,m都是正整数，并且n＞m，求证：对一切x都有2|sinnx-cosnx|≤3|sinnx-cosnx|.

7．在△ABC中，求sinA+sinB+sinC-cosA-cosB-cosC的最大值。

8．求的有的实数a, 使cosa,cos2a,cos4a, …,cos2na, …中的每一项均为负数。

9．已知i，tan1tan2…tann=2,n∈N+, 若对任意一组满足上述条件的

1，2，…，n都有cos1+cos2+…+cosn≤λ，求λ的最小值。