第三章线性方程组(P76)
习题3.1引例与线性方程组(P79)
1.写出下列方程组的矩阵形式:
(1)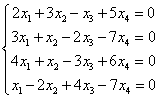 (2)
(2)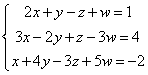
(3)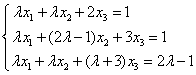
解:(1)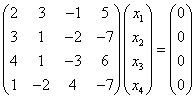 (2)
(2)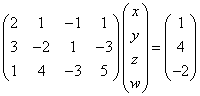
(3)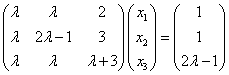
习题3.2齐次线性方程组(P90)
1.求下列齐次线性方程组的一个基础解系和通解:
(1)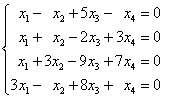
解: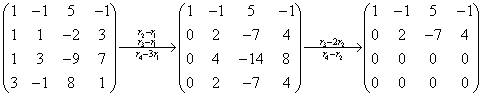
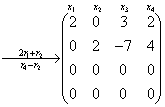
等价方程组: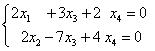 ,分别取
,分别取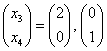 ,得
,得
基础解系: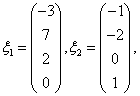
通解: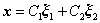 (C1,C2为任意常数)(C1,C2为任意常数)
(C1,C2为任意常数)(C1,C2为任意常数)
(2)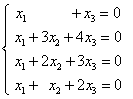
解: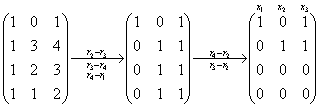
基础解系: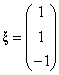 ,通解:
,通解: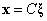 (C为任意常数)
(C为任意常数)
(3)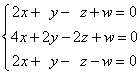
解:
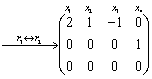
等价方程组为: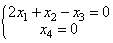 ,分别取
,分别取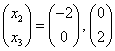 ,得
,得
基础解系: ,通解:
,通解: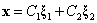 (C1,C2为任意常数)
(C1,C2为任意常数)
(4)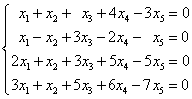
解:
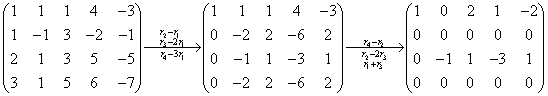
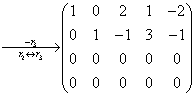
等价方程组: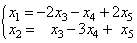 ,分别取
,分别取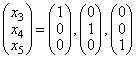 ,得
,得
基础解系: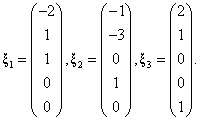
通解: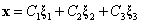 (C1,C2为任意常数)
(C1,C2为任意常数)
2.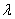 取何值时,方程组
取何值时,方程组
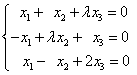
(1)只有零解;
(2)有非零解,并求出其通解。
解: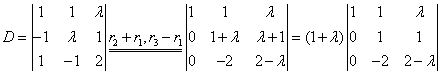

(1)当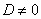 时,即
时,即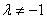 且
且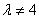 时,方程组只有零解。
时,方程组只有零解。
(2)当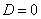 时,即
时,即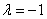 或
或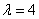 时,方程组有非零解。
时,方程组有非零解。
当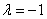 时,
时,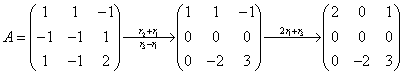
等价方程组: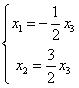 ,取自由未知量
,取自由未知量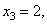 得通解:
得通解: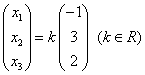
当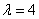 时,
时,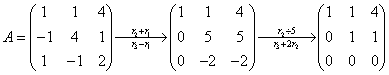
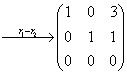
等价方程组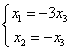 ,取自由未知量
,取自由未知量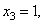 得通解:
得通解: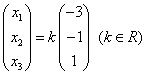
习题3. 3非其次线性方程组(P97)
1.求下列非齐次线性方程组的解:
(1)
解: 对增广矩阵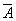 施行初等行变换
施行初等行变换
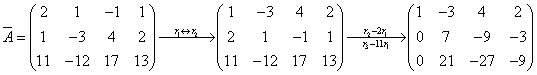
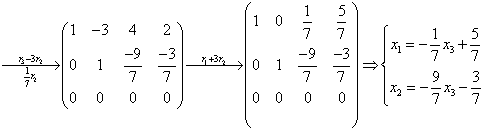
取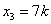 ,得通解:
,得通解: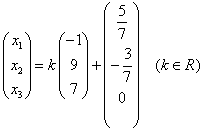
(2)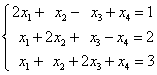
解:对增广矩阵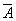 施行初等行变换
施行初等行变换
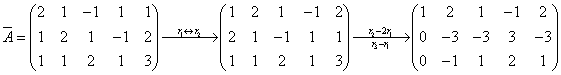
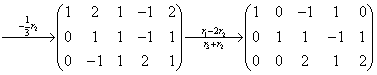

等价方程组: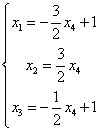 ,取
,取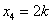 ,得通解:
,得通解: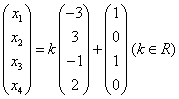
2.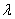 取何值时,非齐次线性方程组
取何值时,非齐次线性方程组
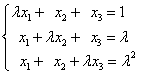
(1)有唯一解;(2)无解;(3)有无穷多解。
解:系数行列式
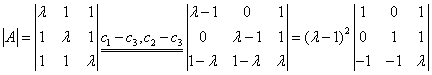
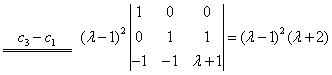
(1)当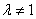 且
且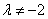 时,
时, ,方程组有唯一解。
,方程组有唯一解。
(2)当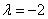 时,增广矩阵
时,增广矩阵
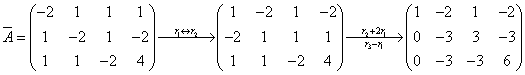
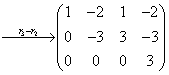
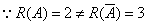 。故无解。
。故无解。
(3)当且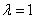 时,
时,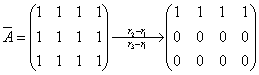
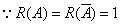 ,故有无穷多解。
,故有无穷多解。
3.设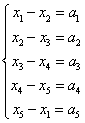
证明该方程组有解的充分必要条件是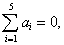 在有解的情况下求其通解。
在有解的情况下求其通解。
解:方程组的增广矩阵是:
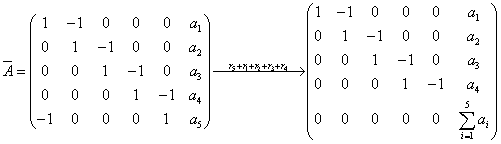
由此可见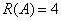 ,方程组有解的充要条件是
,方程组有解的充要条件是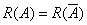 ,而
,而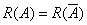 的充要条件是
的充要条件是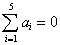 。
。
当方程组有解时,由
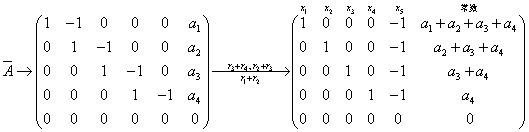
得等价方程组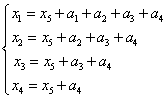 ,取
,取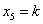 ,得通解:
,得通解:
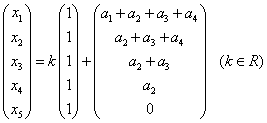
4.设四元非齐次线性方程组的系数矩阵的秩为2,已知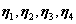 为其四个解向量,且
为其四个解向量,且
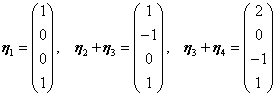
求其通解。
解:设四元非齐次线性方程组为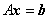 ,对应的齐次线性方程组为
,对应的齐次线性方程组为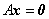 。已知
。已知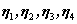 是
是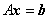 的四个解向量,故有
的四个解向量,故有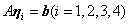 。
。
而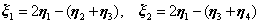 满足
满足
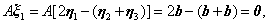
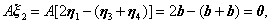
即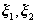 是
是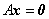 的解。且
的解。且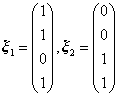 不成比例,故线性无关。
不成比例,故线性无关。
又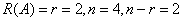 。即
。即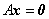 的基础解系由两个线性无关的向量组成,
的基础解系由两个线性无关的向量组成,
故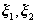 可作为其基础解系,因此
可作为其基础解系,因此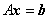 的通解为:
的通解为:
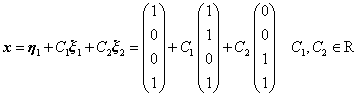
5.设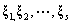 是
是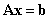 的
的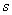 个解,证明:
个解,证明: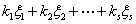 仍是
仍是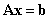 的解,其中
的解,其中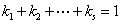 。
。
证明:由于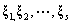 是
是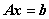 的解,故有
的解,故有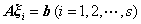
又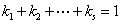 ,则
,则
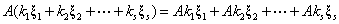

所以,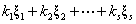 仍是
仍是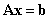 的解
的解
复习题三(P99)
1.设有线性方程组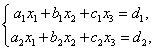 若
若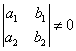 ,问
,问
(1)系数矩阵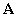 的秩是多少?
的秩是多少?
(2)增广矩阵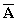 的秩是多少?
的秩是多少?
(3)该方程组是否有解?有多少解?
(4)该方程组对应的齐次线性方程组是否有基础解系?
解:(1)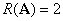
(2)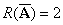
(3) ,该方程组有解。有无穷多解
,该方程组有解。有无穷多解
(4)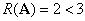 ,所以该方程组对应的齐次线性方程组有基础解系。
,所以该方程组对应的齐次线性方程组有基础解系。
2.确定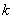 的值,使方程组
的值,使方程组
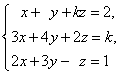
(1) 有唯一的解;(2)无解;(3)有无穷多解。
解:
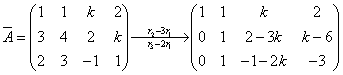
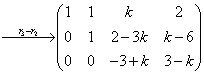
(1) 当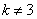 时,
时,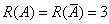 ,方程组有唯一解。
,方程组有唯一解。
(2) 没有无解的情况。
(3) 当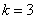 时,
时,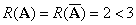 ,有无穷多解。
,有无穷多解。
3.已知方阵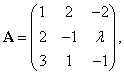
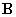 为三阶非零矩阵,且满足
为三阶非零矩阵,且满足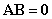 ,试求
,试求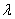 的值。
的值。
解:设三阶非零矩阵B按列分块为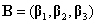 ,不妨设
,不妨设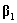 是其非零列,则由
是其非零列,则由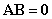
得: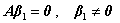
根据A为方阵时,方程组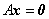 有非零解的充分必要条件是其系数行列式 = 0,
有非零解的充分必要条件是其系数行列式 = 0,
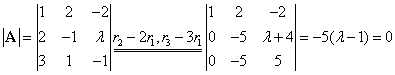
所以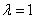 。
。
4.解下列方程组:
(1)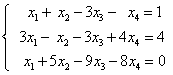
解:(1)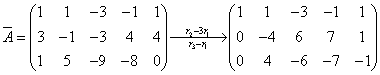
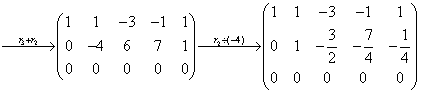
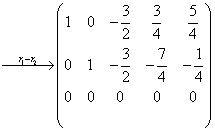
得等价方程组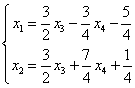 ,取
,取 ,得通解:
,得通解:
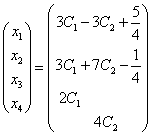
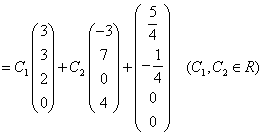
或取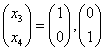 ,代入等价方程组的对应齐次方程组,得到一个基础解系:
,代入等价方程组的对应齐次方程组,得到一个基础解系:
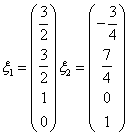 ,并在等价方程组中令
,并在等价方程组中令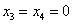 得一个特解:
得一个特解: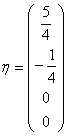 ,
,
故方程组的通解为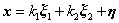 ,
,
即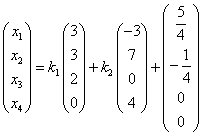
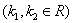
(2)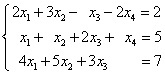
解(2)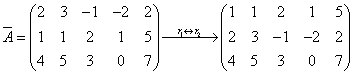
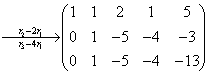

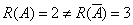 ,方程组无解。
,方程组无解。
(3)
解(3)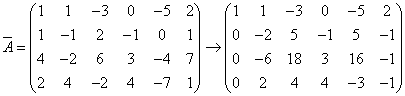
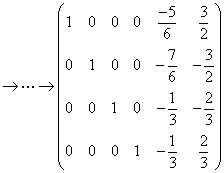
得等价方程组: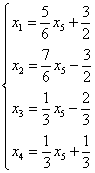 ,取
,取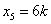 得:
得: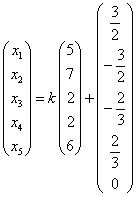

5.设齐次线性方程组
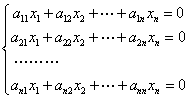
的系数矩阵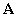 的秩为
的秩为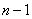 。证明:必有
。证明:必有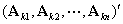 为该齐次线性方程组的一个非零解,其中
为该齐次线性方程组的一个非零解,其中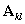 为
为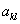 的代数余子式
的代数余子式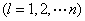 。
。
解:因为系数矩阵A的秩为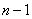 ,所以至少有一个元素的代数余子式不为零,不妨设为
,所以至少有一个元素的代数余子式不为零,不妨设为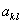 的代数余子式
的代数余子式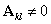 ,取
,取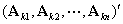 代入方程组,由行列式的性质得
代入方程组,由行列式的性质得
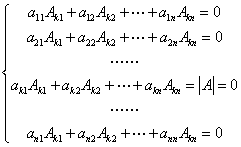 ,
,
即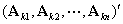 为该齐次线性方程组的一个非零解。
为该齐次线性方程组的一个非零解。
6.试证:含有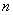 个未知量
个未知量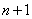 个方程的线性方程组
个方程的线性方程组
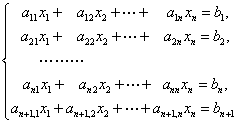
有解的必要条件是行列式
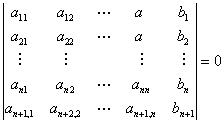 ,
,
但这个条件不是充分的,试举一例。
证明:必要性:即证“方程组有解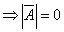 ”
”
因为方程组有解,所以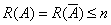 (未知量个数),所以
(未知量个数),所以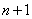 阶行列式
阶行列式
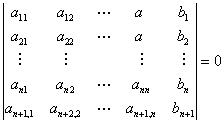
行列式为0不是该方程组有解的充分条件,反例: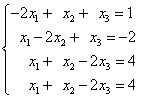
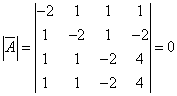 ,但方程组无解。
,但方程组无解。
7.设三维列向量
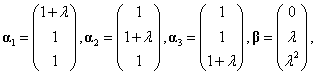
问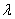 取何值时
取何值时
(1) 有
有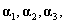 的唯一线性表示式,并写出该表示式;
的唯一线性表示式,并写出该表示式;
(2) 可由
可由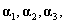 线性表出,但表示式不唯一;
线性表出,但表示式不唯一;
(3) 不能表示成
不能表示成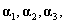 的线性组合。
的线性组合。
解:设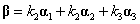 ,对应的非齐次线性方程组的增广矩阵为
,对应的非齐次线性方程组的增广矩阵为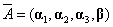

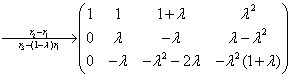
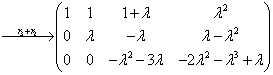
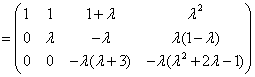
(1) 能由
能由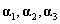 唯一线性表示的充要条件
唯一线性表示的充要条件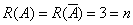 ,
,
故当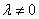 且
且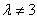 时,
时,
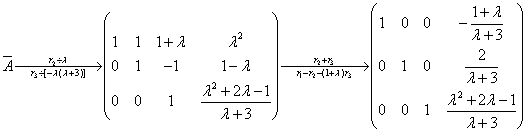
得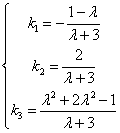 ,故得唯一表示式:
,故得唯一表示式: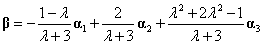
(2) 当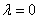 时,
时,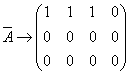
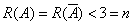 ,
, 可由
可由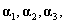 线性表出,但表示式不唯一
线性表出,但表示式不唯一
(3) 当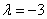 时,
时,
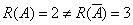 ,即
,即 不能表示成
不能表示成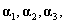 的线性组合。
的线性组合。
8.设有线性方程组
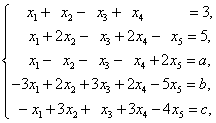
问:(1)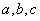 为何值时,方程组无解?
为何值时,方程组无解?
(2)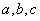 为何值时,方程组有解?
为何值时,方程组有解?
(3)有解时,求其解。
解:对线性方程组的增广矩阵进行初等变换。
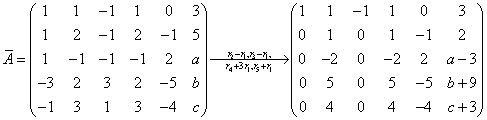
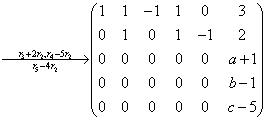
(1) 当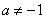 或
或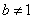 或
或 时,方程组无解。
时,方程组无解。
(2) 当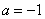 ,
,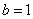 及
及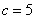 时,方程组有解.
时,方程组有解.
(3) 当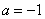 ,
,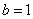 及
及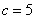 时,方程组的增广矩阵
时,方程组的增广矩阵

得等价方程组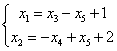 ,令
,令 ,得方程组的通解:
,得方程组的通解:
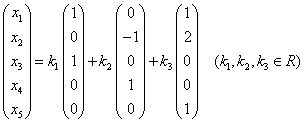
9.设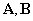 都是
都是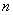 阶方阵,且
阶方阵,且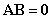 ,证明:
,证明: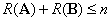 。
。
解:设B按列分块为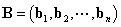 , 则
, 则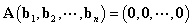
即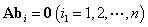 ,
,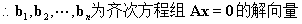
设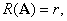 方程组的解空间的秩为
方程组的解空间的秩为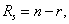 因此
因此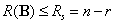 ,
,
故有: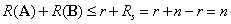
10.设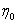 是非齐次线性方程组
是非齐次线性方程组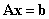 的一个特解,
的一个特解,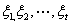 是其导出组的一个基础解系,令
是其导出组的一个基础解系,令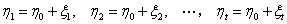
试证该方程组的任一解可表示成如下形式:
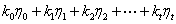
其中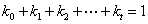
解:设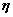 是非齐次线性方程组
是非齐次线性方程组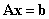 的任一个解,则
的任一个解,则 是对应齐次线性方程组
是对应齐次线性方程组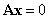 的解,而
的解,而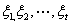 是方程组
是方程组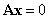 的基础解系,故有
的基础解系,故有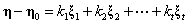
所以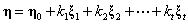
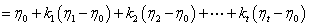
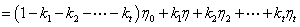
令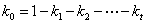 .则得
.则得
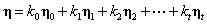 ,其中
,其中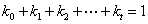
11.设含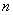 个未知量的非齐次线性方程组
个未知量的非齐次线性方程组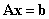 的系数矩阵
的系数矩阵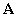 的秩为
的秩为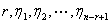 是其
是其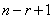 个线性无关的解,试证它的任一解可表示为
个线性无关的解,试证它的任一解可表示为
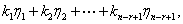
其中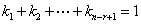
解:首先,对于满足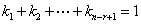 的任意实数
的任意实数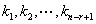 ,有
,有
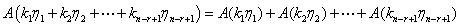
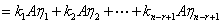
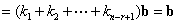 ,
,
因此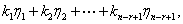 是方程组
是方程组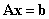 的解.
的解.
其次,作向量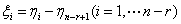 ,则
,则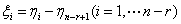 是对应
是对应
齐次方程组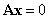 的解,且向量组
的解,且向量组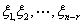 线性无关,因为,若等式
线性无关,因为,若等式
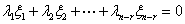 成立,即
成立,即
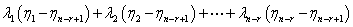
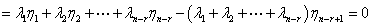
由题设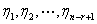 线性无关,因此
线性无关,因此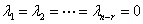 ,故
,故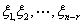 线性无关,因此
线性无关,因此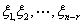 是方程组
是方程组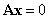 的基础解系,故方程组
的基础解系,故方程组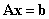 的任一解向量
的任一解向量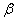 可表示为
可表示为

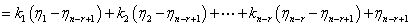
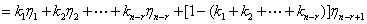
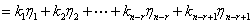
其中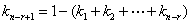 ,即
,即